Що таке інтегрування
Що таке інтегрування
Невизначений інтеграл для функції f — це сукупність усіх первісних цієї функції.
Якщо, задача диференціального числення — знаходження похідної від заданої функції y = f(x), - то задача інтегрального числення протилежна: потрібно визначити функцію, похідна від якої відома. Фундаментальними поняттями інтегрального числення є поняття первісної та невизначеного інтегралу.
Застосування інтегрального числення:
- в задачах про обчислення швидкості або прискорення руху тіла;
- в задачах про обчислення визначених інтегралів (див. формулу Ньютона-Лейбніца);
- при розв'язанні диференціальних рівнянь.
Невизначений інтеграл
Нехай функція F — первісна для f на Х. Невизначеним інтегралом від функції f називається сукупність усіх первісних цієї функції, тобто вираз

де C ∈ J — довільна стала.
Функція f називається підінтегральною функцією, f(x)dx — підінтегральним виразом, C — сталою інтегрування, x — змінною інтегрування.
З геометричної точки зору невизначений інтеграл — це сукупність (сім'я) ліній F(x) + C
Для обчислення невизначених інтегралів використовуються методи:
- Таблиця основних формул інтегрування
- Метод підстановки (або формула заміни змінної)
- Метод інтегрування частинами
Для обчислення невизначених інтегралів використовують такі формули:
Властивості невизначеного інтеграла

Слід відмітити, що справедливість формул інтегрування, а також кожен результат знаходження первісних можна перевірити шляхом диференціювання, оскільки інтегрування — це дія, обернена до диференціювання.
Визначений інтеграл
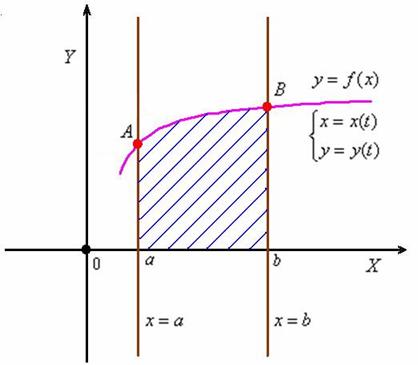
Розглянемо плоску фігуру, обмежену графіком неперервної та невід’ємної на відрізку [a; b] функції f(x), відрізком [a; b], та і прямими x=a та x=b.
Отримана фігура називається криволінійною трапецією. Обчислимо її площу.
Для цього розіб’ємо відрізок [a; b] на n рівних відрізків. Довжини кожного з відрізків дорівнюють Δx.
На кожному відрізку, побудуємо прямокутники з висотами f(xk-1).
Площа кожного такого прямокутника дорівнює Sk = f(xk-1)Δxk.
Площа всіх таких прямокутників дорівнює  .
.
 .
.
Цю суму називають інтегральною сумою для функції f(x).
Якщо n→∞ то площа побудованої таким чином фігури буде все менш відрізнятись від площі криволінійної трапеції.
Границя інтегральної суми коли n→∞ називається визначеним інтегралом, і записується це так : .
.
 .
.
читається: "інтеграл від a до b f від xdx"
Число а називається нижньою межею інтегрування, b – верхньою межею інтегрування, відрізок [a; b] – проміжок інтегрування.
Властивості визначеного інтегралу

Формула Ньютона-Лейбніца
Визначений інтеграл тісно пов’язаний із первісною та невизначеним інтегралом формулою Ньютона- Лейбніца:
 .
.Застосування інтеграла
Інтегральне числення широко використовується при розв’язуванні різноманітних практичних задач. Розглянемо деякі з них.
Обчислення площі криволінійної трапеції
Нехай задано на площині деяку фігуру обмежену лініями x=a, x=b, y=f(x), y=g(x). Тоді її площа буде отримуватись інтегруванням різниці між верхньою та нижньою функцією на даному проміжку
|
Нижньою границею інтегрування треба брати лівий кінець відрізка, на якому визначається криволінійна трапеція.
Обчислення об’ємів тілНехай задана функція, яка задає площу поперечного перерізу тіла в залежності від деякої змінної S = s(x), x [a; b]. Тоді об’єм даного тіла можна знайти проінтегрувавши дану функцію у відповідних межах [a; b]. Тоді об’єм даного тіла можна знайти проінтегрувавши дану функцію у відповідних межах
Якщо нам задане тіло, яке отримане обертанням навколо осі Ох криволінійної трапеції обмеженої деякою функцією f(x), x
 [a; b]. То площі поперечних перерізів можна обчислити за відомою формулою S = π f 2(x). Тому формула об’єму такого тіла обертання [a; b]. То площі поперечних перерізів можна обчислити за відомою формулою S = π f 2(x). Тому формула об’єму такого тіла обертання
Аналогічно для осі Oy, y
При використанні невизначеного інтегралу ми будемо отримувати функцію, а при використанні визначеного – значення певної величини.
Поняття диференціального рівняння
Рівняння, яке містить невідому функцію та її похідні, називається диференціальним рівнянням. Наприклад рівняння yy'+x=0.
Механічний та економічний зміст інтегралу |
Відстань, яку пройде тіло що рухається прямолінійно і змінює свою швидкість за законом v = v(t) за проміжок часу (t0; t1)можна знайти за формулою
Якщо задана залежність продуктивності праці від часу А(t), тоді визначеним інтегралом від даної функції буде кількість продукції виготовленої за проміжок часу (t0; t1)
Приклади
Приклад 1. Знайдіть первісні для функції  .
.
 .
.
Розв’язання
Розв’язання
Розв’язання
Оскільки однією з первісних для функції  є функція
є функція  , то однією з первісних для функції
, то однією з первісних для функції  є
є  ; оскільки однією з первісних для функції sin x є –cos x; первісною
; оскільки однією з первісних для функції sin x є –cos x; первісною  є
є  . Отже,
. Отже,  – первісні для функції
– первісні для функції  .
.
 є функція
є функція  , то однією з первісних для функції
, то однією з первісних для функції  є
є  ; оскільки однією з первісних для функції sin x є –cos x; первісною
; оскільки однією з первісних для функції sin x є –cos x; первісною  є
є  . Отже,
. Отже,  – первісні для функції
– первісні для функції  .
.
Розв’язання
Розв’язання
Приклад 6. Для функції f(х) = sіn х знайдіть первісну, графік якоїпроходить через точку

Розв’язання
Загальний вигляд первісних для функції f(х) = sіn х такий F(х) = -соs х + С.
За умовою графік шуканої первісної проходить через точку

Тому підставляємо π/3 замість х, а -1(1/2) замість F(х) у загальний вигляд первісної, матимемо

Отже, шукана первісна F1(x) = - cos х - 1.
Приклад 7. Обчисліть інтеграл  sіn хdх.
sіn хdх.
Розв’язання
Для функції f(х) = sin х однією з первісних є F(х) = -cos х. Маємо за формулою Ньютона-Лейбніца
Приклад 8. Обчисліть інтеграл
Розв’язання
Спочатку знайдемо первісну для функції f(х) = 2х + 3х2 + 1. Використовуючи правила обчислення первісних та таблицю первісних, маємо:
Матимемо

Зауважимо, що при оформленні цього прикладу знаходження первісної можна було не записувати окремо. Тоді оформлення набуде наступного вигляду:

Приклад 9. Обчисліть інтеграл 
Розв’язання
Використаємо правило 3 знаходження первісних. Маємо

Приклад 10. Знаходження площі фігури, обмеженої графіком

Приклад 11. Очислити об’єм тіла обертання навколо осі абсцис прямих у=х+4, у=2х+1 на відрізку [0,1].
Розв’язання
Шукане тіло знайдемо як різницю тіл утворених обертанням прямої у=х+4 та обертанням прямої у=2х+1. Маємо:

Приклад 12. Продуктивність праці робітника протягом дня задається функцією z(t) = – 0,00645t2 + 0,05t + 0,5 (грош. од./год), де t – час в годинах від початку роботи, 0 ≤ t ≤ 8. Знайти функцію Ǫ = Ǫ(t), яка показує обсяг продукції (у вартісному виразі) та його величину за робочий день.
Розв’язання
Приклад 13. Під дією сили 60 Н пружина розтягується на 0,02м. Яку роботу виконає пружина при видовженні на 0,12 м?
Розв’язання
Застосуємо закон Гука. 0,02к=60, тоді к=3000.
Отже F(x)=3000х
A=1500х2
Приклад 14. Знайти середній час, затрачений на засвоєння одного виробу в період засвоєння від х1=100 до х2=121 виробів, вважаючи в формулі t = ах-b, що а=600 хв, b=0,5.
Розв’язання
Використовуючи формулу середнього часу, отримуємо:

Приклад 15. Вирішити задачу Коші. XУ`+y = XУ2 lnx 

Розв’язання
Розділивши рівняння на Х, отримаємо  Це рівняння вигляду, де N=2, тобто рівняння Бернуллі. Шукаємо рішення у вигляді
Це рівняння вигляду, де N=2, тобто рівняння Бернуллі. Шукаємо рішення у вигляді
 Це рівняння вигляду, де N=2, тобто рівняння Бернуллі. Шукаємо рішення у вигляді
Це рівняння вигляду, де N=2, тобто рівняння Бернуллі. Шукаємо рішення у вигляді
У = і(х)v(x). Тоді У` = U`v + Uv`. Підставимо в рівняння
 Групуємо друге і третє доданки в лівій частині
Групуємо друге і третє доданки в лівій частині  Вибираємо V так, щоб вираз в дужках дорівнював нулю.
Вибираємо V так, щоб вираз в дужках дорівнював нулю.  . Підставимо в рівняння
. Підставимо в рівняння
Загальне рішення 

Підставляємо в загальне рішення початкову умову:

Source: https://formula.kr.ua/pervisna-neviznacheniy-integral/shcho-take-nevyznachenyi-intehral.html

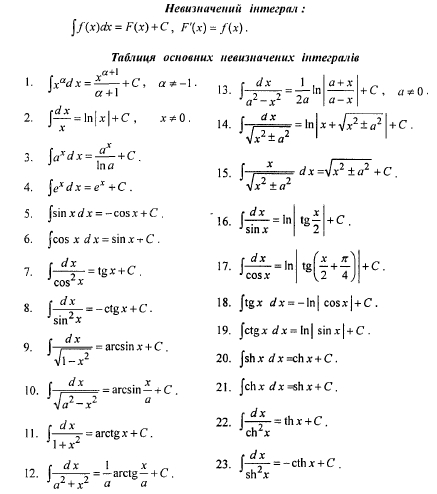
















![\int {\frac{{dx}}{{\sqrt[3]{{3x - 1}}}}} \int {\frac{{dx}}{{\sqrt[3]{{3x - 1}}}}}](http://zno.academia.in.ua/filter/tex/pix.php/458447970eee4b9f97f6ab5baa671f58.png)
![\begin{array}{l}\int {\frac{{dx}}{{\sqrt[3]{{3x - 1}}}}} = \int {{{(3x - 1)}^{ - \frac{1}{3}}}} dx = \frac{1}{3} \cdot \frac{{{{(3x - 1)}^{ - \frac{1}{3} + 1}}}}{{ - \frac{1}{3} + 1}} + C = \frac{1}{3} \cdot \frac{3}{2} \cdot {(3x - 1)^{\frac{2}{3}}} + C = \\ = \frac{1}{2}\sqrt[3]{{{{(3x - 1)}^2}}} + C\end{array} \begin{array}{l}\int {\frac{{dx}}{{\sqrt[3]{{3x - 1}}}}} = \int {{{(3x - 1)}^{ - \frac{1}{3}}}} dx = \frac{1}{3} \cdot \frac{{{{(3x - 1)}^{ - \frac{1}{3} + 1}}}}{{ - \frac{1}{3} + 1}} + C = \frac{1}{3} \cdot \frac{3}{2} \cdot {(3x - 1)^{\frac{2}{3}}} + C = \\ = \frac{1}{2}\sqrt[3]{{{{(3x - 1)}^2}}} + C\end{array}](http://zno.academia.in.ua/filter/tex/pix.php/b17e59186f303cf48f7ac05b9ac7a1c5.png)

Коментарі
Дописати коментар